Quick Start¶
This tutorial aims to explain in a simple way, how to create decision matrices, how to analyze them and how to evaluate them with some multi-criteria analysis methods (MCDA).
Conceptual overview¶
Multi-criteria data are complex. This is because at least two syntactically disconnected vectors are needed to describe a problem.
matrix/\(A\) choice set.And the vector of criteria optimality sense
objectives/\(C\).
Additionally it can be accompanied by a vector w/\(w_j\) with the weighting of the criteria.
To summarize all these data (and some extra ones), Scikit-Criteria provides a DecisionMatrix object along with a mkdm() utility function to facilitate the creation and validation of the data.
Your first DecisionMatrix object¶
First we need to import the the Scikit-Criteria module.
Then we need to create the matrix and objectives vectors.
The matrix must be a 2D array-like where every column is a criteria, and every row is an alternative.
[2]:
# 2 alternatives by 3 criteria
matrix = [
[1, 2, 3], # alternative 1
[4, 5, 6], # alternative 2
]
matrix
[2]:
[[1, 2, 3], [4, 5, 6]]
The objectives vector must be a 1D array-like with number of elements same as number of columns in the alternative matrix (matrix). Every component of the objectives vector represent the optimal sense of each criteria.
[3]:
# let's says the first two alternatives are
# for maximization and the last one for minimization
objectives = [max, max, min]
objectives
[3]:
[<function max>, <function max>, <function min>]
as you see the max and min are the built-in function for find max and mins in collections in python.
As you can see the function usage makes the code more readable. Also you can use as aliases of minimization and maximization the numpy function np.min, np.max, np.amin, np.amax, np.nanmin, np.nanmax; the strings "min", "minimize", "max", "maximize", ">", "<", "+", "-"; and the values -1 (minimize) and 1 (maximize).
Now we can combine this two vectors in our Scikit-Criteria decision matrix.
[4]:
# we use the built-in function as aliases
dm = skc.mkdm(matrix, [min, max, min])
dm
[4]:
| C0[▼ 1.0] | C1[▲ 1.0] | C2[▼ 1.0] | |
|---|---|---|---|
| A0 | 1 | 2 | 3 |
| A1 | 4 | 5 | 6 |
As you can see the output of the DecisionMatrix object is much more friendly than the plain python lists.
To change the generic names of the alternatives (A0 and A1) and the criteria (C0, C1 and C2); let’s assume that our data is about cars (car 0 and car 1) and their characteristics of evaluation are autonomy (\(maximize\)), comfort (\(maximize\)) and price (\(minimize\)).
To feed this information to our DecisionMatrix object we have the parameters: alternatives that accept the names of alternatives (must be the same number as the rows that matrix has), and criteria the criteria names (must have same number of elements with the columns that matrix has)
[5]:
dm = skc.mkdm(
matrix,
objectives,
alternatives=["car 0", "car 1"],
criteria=["autonomy", "comfort", "price"],
)
dm
[5]:
| autonomy[▲ 1.0] | comfort[▲ 1.0] | price[▼ 1.0] | |
|---|---|---|---|
| car 0 | 1 | 2 | 3 |
| car 1 | 4 | 5 | 6 |
In our final step let’s assume we know in our case, that the importance of the autonomy is the 50%, the comfort only a 5% and the price is 45%. The param to feed this to the structure is called weights and must be a vector with the same elements as criterias on your alternative matrix (number of columns).
[6]:
dm = skc.mkdm(
matrix,
objectives,
weights=[0.5, 0.05, 0.45],
alternatives=["car 0", "car 1"],
criteria=["autonomy", "comfort", "price"],
)
dm
[6]:
| autonomy[▲ 0.50] | comfort[▲ 0.05] | price[▼ 0.45] | |
|---|---|---|---|
| car 0 | 1 | 2 | 3 |
| car 1 | 4 | 5 | 6 |
Manipulating the Data¶
The data object are immutable, if you want to modify it you need create a new one. All the data are stored as pandas dataframes and numpy arrays
You can access to the different parts of your data, simply by typing dm.<your-parameter-name> for example:
[7]:
dm.matrix # note how this data ignores the objectives and the weights
[7]:
| Criteria | autonomy | comfort | price |
|---|---|---|---|
| Alternatives | |||
| car 0 | 1 | 2 | 3 |
| car 1 | 4 | 5 | 6 |
[8]:
dm.objectives
[8]:
autonomy MAX
comfort MAX
price MIN
Name: Objectives, dtype: object
[9]:
dm.weights
[9]:
autonomy 0.50
comfort 0.05
price 0.45
Name: Weights, dtype: float64
[10]:
dm.alternatives, dm.criteria
[10]:
(_ACArray(['car 0', 'car 1'], dtype=object),
_ACArray(['autonomy', 'comfort', 'price'], dtype=object))
If you want (for example) change the names of the cars from car 0 and car 1; to VW and Ford you must the copy method and provide the new names:
[11]:
dm = dm.copy(alternatives=["VW", "Ford"])
dm
[11]:
| autonomy[▲ 0.50] | comfort[▲ 0.05] | price[▼ 0.45] | |
|---|---|---|---|
| VW | 1 | 2 | 3 |
| Ford | 4 | 5 | 6 |
Note:
For more complex matiluations you can use the dm.iloc[x], dm.loc[x] and dm[x] interface.
Plotting¶
The Data structure support some basic routines for plotting.
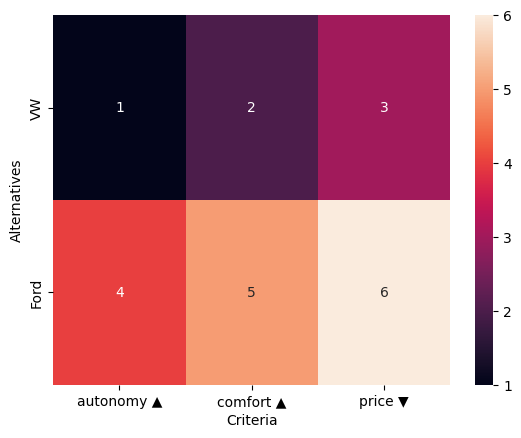
The default scikit criteria uses the Heatmap plot to visualize all the data.
[12]:
dm.plot()
[12]:
<AxesSubplot:xlabel='Criteria', ylabel='Alternatives'>
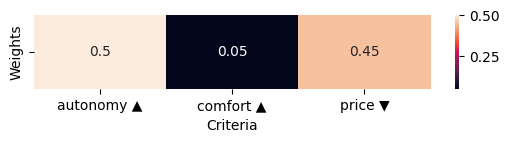
In the same fashion you can plot the weights of the criteria
[13]:
dm.plot.wheatmap()
[13]:
<AxesSubplot:xlabel='Criteria'>
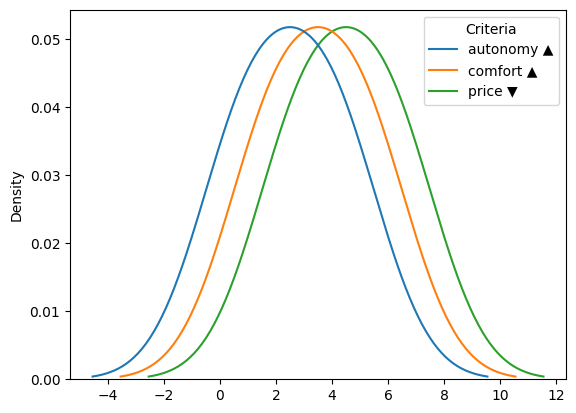
You can accessing the different kind of plot by passing the name of the plot as first parameter of the method
[14]:
dm.plot("kde")
[14]:
<AxesSubplot:ylabel='Density'>
or by using the name as method call inside the plot attribute
[15]:
dm.plot.kde()
[15]:
<AxesSubplot:ylabel='Density'>
Every plot has their own set of parameters, defined by the subjacent function
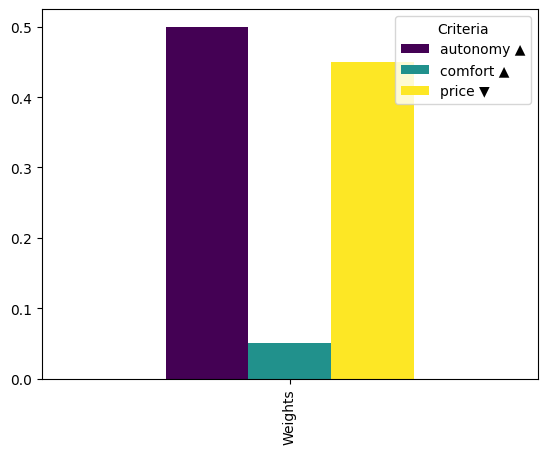
Let’s change the colors of the weight bar plot and show:
[16]:
dm.plot.wbar(cmap="viridis")
[16]:
<AxesSubplot:>
Data transformation¶
Data in its current form is difficult to understand and analyze. On one hand they are out of scale, and on the other they have both minimizing and maximizing criteria.
Note: Scikit-Criteria objective preference
For a design decision Scikit-Criteria always prefers Maximize objectives. There are some functionalities that trigger warnings against Minimize criteria, and others that directly and others directly fail.
To solve these problems, we will use two processors:
First
InvertMinimizewhich inverts the minimizing objectives. by dividing out the inverse of each criterion value (\(1/C_j\)).Second,
SumScalerwhich will divide each criterion value by the total sum of the criteria, taking all of them into the range \([0, 1]\).
First we start by importing the two necessary modules.
[17]:
from skcriteria.preprocessing import invert_objectives, scalers
Data in its current form is difficult to understand and analyze. The first thing we must do now is to reverse the maximization criteria.
This involves:
Create the transformer and store it in the
invertervariable.Apply the transformation by calling the
transformmethod of the transformer and passing it as parameter our decision matrixdm.Save the transformed decision matrix in a new variable
dmt.
In code:
[18]:
inverter = invert_objectives.InvertMinimize()
dmt = inverter.transform(dm)
dmt
[18]:
| autonomy[▲ 0.50] | comfort[▲ 0.05] | price[▲ 0.45] | |
|---|---|---|---|
| VW | 1 | 2 | 0.333333 |
| Ford | 4 | 5 | 0.166667 |
The next step is to scale the values between \([0, 1]\) using the SumScaler.
For this step we need
Create the transformer and store it in the
invertervariable. In this case the scalers support a parameter calledtargetwhich can have three different values:target="matrix"The matrix \(A\) is normalized.target="weights"normalizes the weights \(w\).target="both"normalizes matrix \(A\) and weights \(w\).
In our case we are going to ask the scaler to scale both components of the decision matrix (
target="both")Apply the transformation by calling the
transformmethod of the transformer and passing it as parameter our decision matrixdmt.Save the transformed decision by overwriting the variable
dmt.
[19]:
scaler = scalers.SumScaler(target="both")
dmt = scaler.transform(dmt)
dmt
[19]:
| autonomy[▲ 0.50] | comfort[▲ 0.05] | price[▲ 0.45] | |
|---|---|---|---|
| VW | 0.2 | 0.285714 | 0.666667 |
| Ford | 0.8 | 0.714286 | 0.333333 |
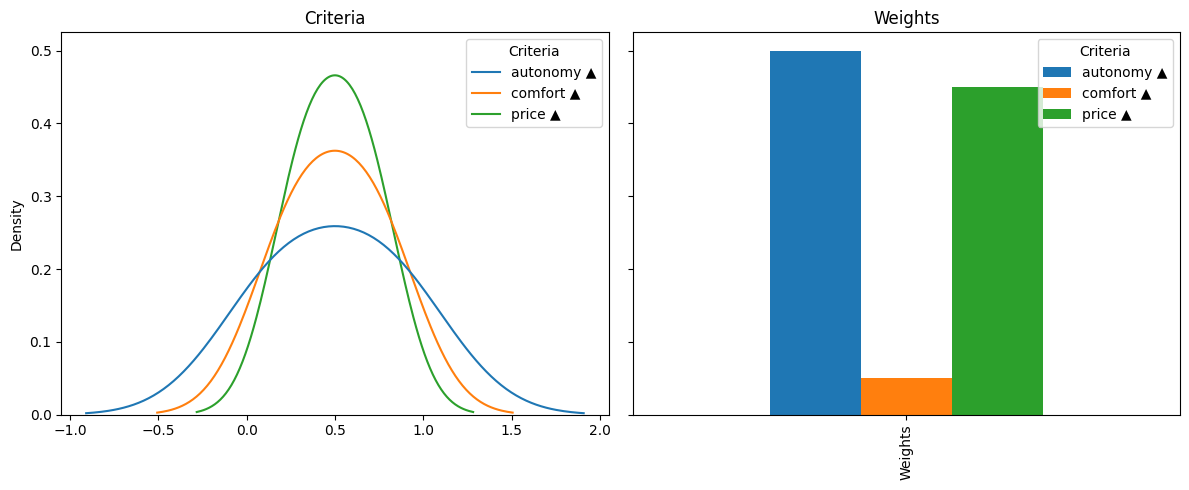
Now we can analyze if the matrix graphically by creating a graph for the matrix, and another for the weights.
Note: Advanced plots with Matplotlib
If you need more information on how to make graphs using Matplotlib please che this tutorial https://matplotlib.org/stable/tutorials/index
[20]:
# we are going to user matplotlib capabilities of creat multiple figures
import matplotlib.pyplot as plt
# we create 2 axis with the same y axis
fig, axs = plt.subplots(1, 2, figsize=(12, 5), sharey=True)
# in the first axis we plot the criteria KDE
dmt.plot.kde(ax=axs[0])
axs[0].set_title("Criteria")
# in the second axis we plot the weights as bars
dmt.plot.wbar(ax=axs[1])
axs[1].set_title("Weights")
# adjust the layout of the figute based on the content
fig.tight_layout()
Using this data to feed some MCDA methods¶
Weighted Sum Model¶
Let’s rank our dummy data by Weighted Sum Model
First we need to import the required module
[21]:
from skcriteria.agg import simple
To use the methods of MCDA structure we proceed in the same way as when using transformers:
We create the decision maker and store it in some variable (
decin our case).Execute the
evaluate()method inside the decision maker to create the result.We store the result in some variable (
rankin our case).
Note: Hyper-parameters
Some multi-criteria methods support “hyper parameters”, which are provided at the time of creation of the decision maker.
We will see an example with the ELECTRE-1 method later on.
[22]:
dec = simple.WeightedSumModel()
rank = dec.evaluate(dmt) # we use the tansformed version of the data
rank
[22]:
| Alternatives | VW | Ford |
|---|---|---|
| Rank | 2 | 1 |
We can see that WeightedSumModel prefers the alternative Ford over the VW.
We can access the intermediate calculators of the method through the e_ attribute of the result object., which (in the case of WeightedSumModel) contains the resulting scores
[23]:
rank.e_
[23]:
<extra {'score'}>
[24]:
rank.e_.score
[24]:
array([0.41428571, 0.58571429])
Obviously you can acces all the parts of the ranking as attributes of result object
[25]:
rank.rank_
[25]:
array([2, 1])
[26]:
rank.alternatives
[26]:
array(['VW', 'Ford'], dtype=object)
[27]:
rank.method
[27]:
'WeightedSumModel'
Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)¶
The following example will be approached with the TOPSIS. This method was chosen because of its popularity and because it uses another scaling technique (VectorScaler).
So the first thing one would intuitively do is to invert the original matrix criteria (dm) and then apply the normalization; but if we have several matrices or several methods this solution becomes cumbersome.
The proposed solution of Scikit-Criteria is to offer pipelines. The pipelines combine one or several transformers and one decision-maker the facilitate the execution of the experiments.
So, let’s import the necessary modules for TOPSIS and the pipelines:
Distances and InvertMinimize
Since TOPSIS uses distances as a comparison metric, it is not recommended to use the InvertMinimize transformer. Instead we use NegateMinimize.
[28]:
from skcriteria.agg import similarity # here lives TOPSIS
from skcriteria.pipeline import mkpipe # this function is for create pipelines
The trick is that the weights still need to be scaled with SumScaler so be careful to assign the targets correctly in each transformer.
[29]:
pipe = mkpipe(
invert_objectives.NegateMinimize(),
scalers.VectorScaler(target="matrix"), # this scaler transform the matrix
scalers.SumScaler(target="weights"), # and this transform the weights
similarity.TOPSIS(),
)
pipe
[29]:
<SKCPipeline [steps=[('negateminimize', <NegateMinimize []>), ('vectorscaler', <VectorScaler [target='matrix']>), ('sumscaler', <SumScaler [target='weights']>), ('topsis', <TOPSIS [metric='euclidean']>)]]>
Now we can directly call the pipeline evaluate() method with the original decision-matrix (dm).
This method sequentially executes the three transformers and finally the evaluator to obtain a result
[30]:
rank = pipe.evaluate(dm)
rank
[30]:
| Alternatives | VW | Ford |
|---|---|---|
| Rank | 2 | 1 |
[31]:
print(rank.e_)
print("Ideal:", rank.e_.ideal)
print("Anti-Ideal:", rank.e_.anti_ideal)
print("Similarity index:", rank.e_.similarity)
<extra {'similarity', 'ideal', 'anti_ideal'}>
Ideal: [ 0.48507125 0.04642383 -0.20124612]
Anti-Ideal: [ 0.12126781 0.01856953 -0.40249224]
Similarity index: [0.35548671 0.64451329]
Where the ideal and anti_ideal are the normalizated sintetic better and worst altenatives created by TOPSIS, and the similarity is how far from the anti-ideal and how closer to the ideal are the real alternatives
ÉLimination et Choix Traduisant la REalité (ELECTRE)¶
For our final example, we are going to use the method ELECTRE-I which has two particularities:
It does not return a ranking but a kernel.
It supports two hyper-parameters: a concordance threshold
pand a discordance thresholdq.
Let’s test the default threshold (p=0.65, q=0.35) but with two normalizations for different matrix: VectorScaler and SumScaler.
For this we will make two pipelines
[32]:
from skcriteria.agg import electre
pipe_vector = mkpipe(
invert_objectives.InvertMinimize(),
scalers.VectorScaler(target="matrix"), # this scaler transform the matrix
scalers.SumScaler(target="weights"), # and this transform the weights
electre.ELECTRE1(p=0.65, q=0.35),
)
pipe_sum = mkpipe(
invert_objectives.InvertMinimize(),
scalers.SumScaler(target="weights"), # transform the matrix and weights
electre.ELECTRE1(p=0.65, q=0.35),
)
[33]:
kernel_vector = pipe_vector.evaluate(dm)
kernel_vector
[33]:
| Alternatives | VW | Ford |
|---|---|---|
| Kernel | True | True |
[34]:
kernel_sum = pipe_sum.evaluate(dm)
kernel_sum
[34]:
| Alternatives | VW | Ford |
|---|---|---|
| Kernel | True | True |
As can be seen for this case both scalings give the same results
Generated by nbsphinx from a Jupyter notebook. 2024-02-10T20:35:33.978285